Tag Archives: Convolution

Examples of convolution (continuous case)

By Dan Ma on | 12 Comments

The method of convolution is a great technique for finding the probability density function (pdf) of the sum of two independent random variables. We state the convolution formula in the continuous case as well as discussing the thought process. Some examples are provided to demonstrate the technique and are followed by an exercise.

The Convolution Formula (Continuous Case)
Let X and Y be independent continuous random variables with pdfs f_X(x) and f_Y(y), respectively. Let Z=X+Y. Then the following is the pdf of Z.

\displaystyle \begin{aligned}f_Z(z)&=\int_{-\infty}^\infty f_Y(z-x) f_X(x) \ dx \\&=\int_{-\infty}^\infty f_X(z-y) f_Y(y) \ dy \end{aligned}

Let’s look at the thought process behind the formula. Since X and Y are independent, the joint pdf of X and Y is f_{X,Y}(x,y)=f_X(x) \ f_Y(y). The pdf of Z is simply the sum of the “joint density” at the points of the line z=x+y. In Figure 1 below, every point at the line z=x+y is of the form (x,z-x). The joint density at each such point is f_X(x) \ f_Y(z-x). Summing the values of these joint density produces the probability density function of Z.

Setting the limits of the integral depends on knowing the range of possible values of x or y for a given line z=x+y. If X and Y can only take on positive values, then for a given line z=x+y, both x or y can range from 0 to z (see Example 1 below).

Example 1
Let X and Y be independent exponentially distributed variables with common density f(x)=\alpha e^{-\alpha x} where \alpha>0. Then the following is the pdf of Z=X+Y.

\displaystyle \begin{aligned}f_Z(z)&=\int_{0}^z f_Y(z-x) f_X(x) \ dx \\&=\int_{0}^z \alpha e^{-\alpha (z-x)} \alpha e^{-\alpha x} \ dx \\&=\int_{0}^z \alpha^2 e^{-\alpha z} \ dx =\alpha^2 \ z \ e^{-\alpha z} \end{aligned}

The above pdf indicates that the independent sum of two identically distributed exponential variables has a Gamma distribution with parameters 2 and \alpha.

Example 2
Let X and Y be independent uniformly distributed variables, U(0,10) and U(0,20), respectively. The pdf of Z=X+Y is:

\displaystyle f_Z(z)=\left\{\begin{matrix} \displaystyle \frac{z}{200}&\ \ \ \ \ \ 0 \le z <10 \\{\text{ }}& \\{\displaystyle \frac{1}{20}}&\ \ \ \ \ \ 10 \le z <20 \\{\text{ }}& \\{\displaystyle \frac{30-z}{200}}&\ \ \ \ \ \ 20 \le z <30 \end{matrix}\right.

The convolution formula is applied three times. For the first case, the line x+y=z ranges in 0 \le z < 10. For each such line, we have 0<x<z. Figure 2 below is a representative diagram.

\displaystyle \begin{aligned}f_Z(z)&=\int_{0}^{z} f_Y(z-x) f_X(x) \ dx \\&=\int_{0}^{z} \frac{1}{20} \frac{1}{10} \ dx =\frac{z}{200} \end{aligned}

For the second case, the line x+y=z ranges in 10 \le z < 20. For each such line, x ranges from 0 to 10. Figure 3 below is a representative diagram.

\displaystyle \begin{aligned}f_Z(z)&=\int_{0}^{10} f_Y(z-x) f_X(x) \ dx \\&=\int_{0}^{10} \frac{1}{10} \frac{1}{20} \ dx =\frac{1}{20} \end{aligned}

For the third case, the line x+y=z ranges in 20 \le z < 30. Figure 4 below is a representative diagram.

\displaystyle \begin{aligned}f_Z(z)&=\int_{z-20}^{10} f_Y(z-x) f_X(x) \ dx \\&=\int_{z-20}^{10} \frac{1}{10} \frac{1}{20} \ dx =\frac{30-z}{200} \end{aligned}

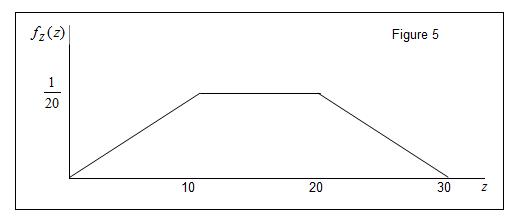
The following is the graph of the pdf of Z=X+Y.

Exercise
Suppose that X is an exponentially distributed variable with pdf f(x)=\alpha e^{-\alpha x} and Y has the uniform distribution U(0,1). Find the pdf of the independent sum Z=X+Y.

\displaystyle f_Z(z)=\left\{\begin{matrix} \displaystyle 1-e^{-\alpha z}&\ \ \ \ \ \ 0 \le z <1 \\{\text{ }}& \\{\text{ }}& \\{\displaystyle e^{-\alpha z}(e^\alpha-1)}&\ \ \ \ \ \ 1 \le z <\infty \end{matrix}\right.

Posted in: Independent Sum | Tagged: , , ,